adapted from http://deeplearning.net/software/theano/tutorial/
Theano Tutorial
Basic Algebra
Adding two scalars
import theano.tensor as T
from theano import function
x = T.fscalar('x')
y = T.fscalar('y')
By calling T.dscalar with a string argument, we create a variable representing a floating-point scalar quantity with the given name.
z = x + y
z is another variable representing the addition of x and y. We can use pp function to pretty-print out the computation associate with z:
from theano import pp
print(pp(z))
The last step is to create a function taking x and y as inputs and giving z as output:
f = function([x, y], z)
The first argument to function is a list of variables that will be provided as inputs to the function. The second argument is a single variable or a list of variables. For either case, the second argument is what we want to see as output when we apply the function. f may then be used like a normal Python function.
Adding two matrices
x = T.fmatrix('x')
y = T.fmatrix('y')
z = x + y
f = function([x, y], z)
More examples
http://deeplearning.net/software/theano/tutorial/examples.html
Logistic function
For logistic function, :
x = T.fmatrix('x')
s = 1 / (1 + T.exp(-x))
# even for ONE argument, we have to use []
logistic = function([x], s)
Setting a default value for an argument
from theano import Param
x, y = T.fscalars('x', 'y')
z = x + y
f = function([x, Param(y, default=1)], z)
f(10)
Using shared variables
For example, we want to make an accumulator: at the beginning, the state is initialized to zero. Then, on each function call, the state is incremented by the function's argument.
Let's first define the accumulator function. It adds its argument to the internal state, and returns the OLD state value:
from theano import shared
state = shared(0)
inc = T.iscalar('inc')
accumulator = function([inc], state, updates=[(state, state+inc)])
The shared function constructs shared variables. Their value may be shared between multiple functions. The value can be accessed and modified by .get_value() and .set_value() methods.
As a parameter of function, updates must be supplied with a list of pairs of the form (shared-variable, new expression). It can also be a dictionary whose keys are shared-variables and values are the new expressions. It means "whenever this function runs, it will replace the .value of each shared variable with the result of the corresponding expression". Above, the accumulator replaces the state value with the sum of the state and the increment amount.
.set_value() can be used to reset the state.
Why we need theano.shared? For efficiency. Updates to shared variables can sometimes be done more quickly using in-place algorithms. Also, Theano has more control over where and how shared variables are allocated, which is important for GPU.
Using random numbers
The way to think about putting randomness into Theano's computations is to put random variables in the graph. Theano will allocate a Numpy RandomStream object (a random number generator) for each such variable, and draw from it as necessary. This sort of sequence of random numbers are called a random stream. Random streams are at their core shared variables, so the observations on shared variables hold here as well.
An example is:
from theano.tensor.shared_randomstreams import RandomStreams
from theano import function
srng = RandomStreams(seed=234)
rv_u = srng.uniform((2,2))
rv_n = srng.normal((2, 2))
f = function([], rv_u)
g = funciton([], rv_n, no_default_updates=True) # not updating rv_n.rng
nearly_zeros = function([], rv_u + rv_u - 2 * rv_u)
rv_u is a random straem of 2x2 matrices of draws from a uniform distribution. rv_n is a random stream of 2x2 matrices of draws from a normal distribution.
An important remark is that a ranodm variable is drawn at most once during any single function execution. So the nearly_zeros function is guaranteed to return approximately 0 even though the rv_u random variable appears three times in the output expression.
seeding streams
We can seed one random variable by seeding or assigning to the .rgn attribute, using .rng.set_value()
rng_val = rv_u.rng.get_value(borrow=True) # get the rng for rv_u
rng_val.seed(12345) # seed the generator
rv_u.rng.set_value(rng_val, borrow=True) # assign back seeded rng
sharing streams between functions
a bit TRICKY example
state_after_v0 = rv_u.rng.get_value().get_state()
v0 = f()
v1 = f()
rng = rv_u.rng.get_value(borrow=True)
rng.set_state(state_after_v0)
rv_u.rng.set_value(rng, borrow=True)
v2 = f() # v2 == v0
v3 = f() # v3 == v1
Copying random state between Theano graphs
Graph structures
The first step in writing Theano code is to write down all mathematical relations using symbolic placeholders (variables). When writing down these expressions you use operations like +, -, *, sum(), tanh(). All these are represented internally as ops*. An op represents a certain computation on some type of inputs producing some type of output. You can see it as a function definition in most programming languages.
Theano builds internally a graph structure composed of interconnected variable nodes, opnodes and apply nodes. An apply node represents the application of an op to some variables.
x = T.fmatrix('x')
y = T.fmatrix('y')
z = x + y
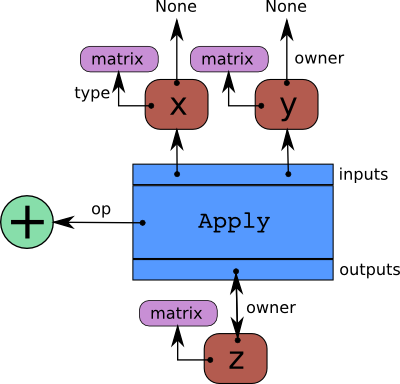
The graph can be traversed starting from outputs (the result of some computation) down to its inputs using the owner field.
Automatic differentiation
tensor.grad() will traverse the graph from the outputs back towards the inputs through all apply nodes (apply nodes are those that define which computations the graph does). For each such apply node, its op defines how to compute the gradient of the node's outputs with respect to its inputs.
Derivatives in Theano
Computing the gradient
Say we want to compute :
from theano import pp
x = T.fscalar('x')
y = x ** 2
gy = T.grad(y, x)
print(pp(gy))
f = function([x], gy)
From print(pp(gy)) we can see that fill((x ** TensorConstant{2}), TensorConstant{1.0}), which means to make a matrix of the same shame as x**2 and fill it with 1.0.
Computing the Jacobian
Jacobian designates the tensor comprising the first partial derivatives of the output of a function with respect to its inputs. theano.gradient.jacobian() will do it automatically
Loop
Simple loop with accumulation: computing $A^{k}$
Given k we want to get A**k using a loop:
result = 1
for i in xrange(k):
result = result * A
There are three things to notice: the initial value assigned to result, the accumulation of results in result, and the unchanging variable A. Unchanging variables are passed to scan as non_sequences. Initialization occurs in outputs_info, and the accumulation happens automatically.
The equivalent Theano code is:
k = T.iscalar('k')
A = T.vector('A')
result, updates = theano.scan(fn=lambda prior_result, A: prior_result * A, outputs_info=T.ones_like(A), non_sequences=A, n_steps=k)
# We only care about A**k, but scan has provided us with A**1 through A**k.
# Discard the values that we don't care about. Scan is smart enough to
# notice this and not waste memory saving them.
final_result = result[-1]
# compiled function that returns A**k
power = theano.function(inputs=[A,k],
outputs=final_result, updates=updates)
print(power(range(10),2))
print(power(range(10),4))
Within theano.scan, the order of parameters to fn is fixed: the output of the prior call to fn(or the initial value, initially) is the first parameter, followed by all non-sequences.
Next we initialize the output as a tensor with the same shape and dtype as A, filled with ones. We give A to scan as a non-sequences parameter and specify the number of steps k to iterate over our lambda expression.
theano.scan returns a tuple containing our result (result) and a dictionary of updates (empty in this case). The result is a 3D tensor containing the value of A**k for each step. We want the last value so we compile a function to return just that. Due to the internal optimization, we don't have to worry if A or k is large.
Iterating over the first dimension of a tensor: Calculating a polynomial
theano.scan can iterate over the leading dimension of tensors (similar to for x in a_list).
The tensor to be looped over should be provided to scan using the sequence keyword argument.
Here’s an example that builds a symbolic calculation of a polynomial from a list of its coefficients:
coefficients = theano.tensor.vector("coefficients")
x = T.scalar("x")
max_coefficients_supported = 10000
# Generate the components of the polynomial
components, updates = theano.scan(fn=lambda coefficient, power, free_variable: coefficient * (free_variable ** power),
outputs_info=None,
sequences=[coefficients, theano.tensor.arange(max_coefficients_supported)],
non_sequences=x)
# Sum them up
polynomial = components.sum()
# Compile a function
calculate_polynomial = theano.function(inputs=[coefficients, x], outputs=polynomial)
# Test
test_coefficients = numpy.asarray([1, 0, 2], dtype=numpy.float32)
test_value = 3
print calculate_polynomial(test_coefficients, test_value)
print 1.0 * (3 ** 0) + 0.0 * (3 ** 1) + 2.0 * (3 ** 2)
There is no accumulation of results, we can set outputs_info to None. This indicates to scan that it doesn't need to pass the prior result to fn.
The general order of function parameters to fn is:
sequences (if any), prior result(s) (if needed), non-sequences (if any)
In sequences=[coefficients,T.arange(max_coefficients_supported)], scan will truncate to the shortest of them.
Simple accumulation into a scalar, ditching lambda
The following example stresses a pitfall to be careful: the initial outputs_info must be of a shape similar to that of the output variable generated at each iteration and moreover, it must not involve an implicit downcast of the latter.