• Recursion
  • Examples
    • Factorial function
    • English Ruler (Fractal)
    • Binary Search
    • File Systems
  • Recursion Run Amok

Recursion

Code and descriptions are mainly adapted from [Data Structures and Algorithms in Python].

Recursion makes one or more calls to itself during execution, or by which a data structure relies upon smaller instances of the very same type of structure in its representation.

Examples

Factorial function

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

Repetition is provided by the repeated recursive invocation of the function.

English Ruler (Fractal)

Fractal is a shape that has a self-recursive structure at various levels of magnification.

Due to the symmetry, an interval with a central tick length $L\geq1$ is composed of:

• An interval with a central tick length $L-1$
• A single tick of length $L$
• An interval with a central tick length $L-1$

[Data Structures and Algorithms in Python], p154, Figure 4.3

# this reminds me of depth-first tree traverse
def draw_line(tick_length, tick_label=''):
     line = '-' * tick_length
     if tick_label:
         line += ' ' + tick_label
        print(line)

def draw_interval(center_length):
    if center_length > 0:
        draw_interval(center_length - 1)
        draw_line(center_length)
        draw_interval(center_length - 1)    

def darw_ruler(num_inches, major_length):
    draw_line(major_length, '0')
    for j in range(1, 1 + num_inches):
        draw_interval(major_length - 1)
        draw_line(major_length, str(j))

time complexity: For $c\geq0$, a call to draw_interval(c) results in precisely $2^{c}-1$ lines of output.

Binary Search

The following is code2flow:

binary_search:
nop;
binary_search(data, target, low, high);
if(low>high) {
  False;
  return;
}
else{
  mid=(low+high)//2;
  if(target==data[mid]) {
    True;
    return;
  }
  else if(target<data[mid]) {
    //recursion
    binary_search(data, target, low, mid-1);
    loop binary_search;
  }
  else{
    //recursion
    binary_search(data, target, mid+1, high);
    loop binary_search;}
}

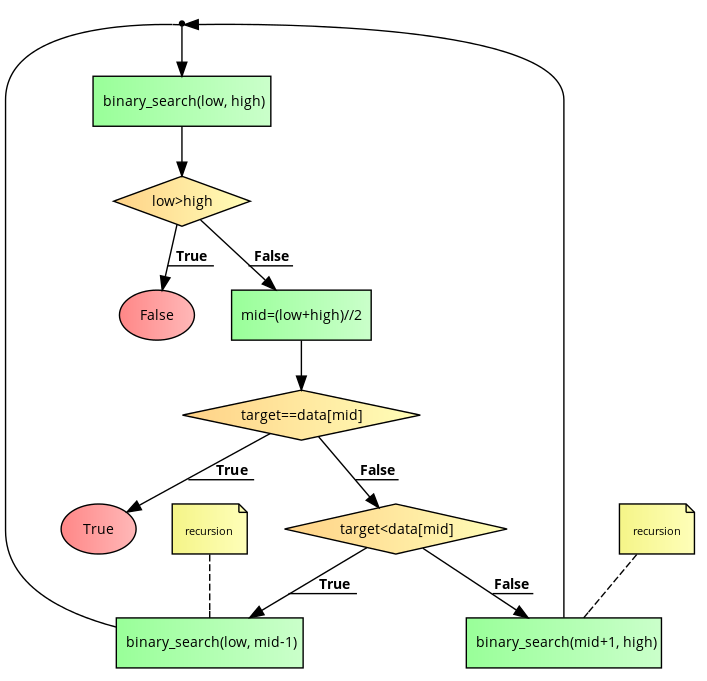
The Python code is:

def binary_search(data, target, low, high):
    if low > high:
        return False:
    else:
        mid = (low+high) // 2
        if target == data[mid]:
            return True:
        elif target < data[mid]:
            return binary_search(data, target, low, mid -1)
        else:
            return binary_search(data, target, mid + 1, high)

Time complexity: $O(\mathrm{log}n)$ for a sorted sequence with n elements.

File Systems

The code for code2flow:

recursion:
//recursion call
nop
**DiskUsage**(path);
//immediate disk space of current entry
total=size(path);
if(path represents a directory?){
  while(has child entry in directory path?){
    total+=**DiskUsage**(child);
    loop recursion;
  }
}
Return total;
return;

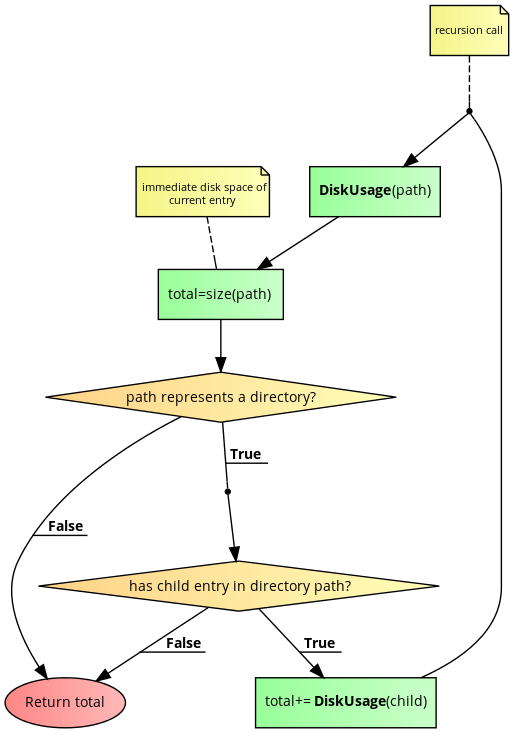
The file system's tree structure is:

The actual execution order is:

As can be seen, it is depth first. The Python code is:

import os
def disk_usage(path):
    total = os.path.getsize(path)
    if os.path.isdir(path):
        for file_name in os.listdir(path):
            child_path = os.path.join(path, file_name)
            total += disk_usage(child_path)
    print('{0:<7}'.format(total), path)
    return total

Recursion Run Amok

Element uniqueness problem using for:

def unique1(S):
    for j in range(len(S)):
        for k in range(j+1, len(S)):
            if S[j] == S[k]:
                return False
    return True

def unique2(S):
    temp = sorted(S)
    for j in range(len(S)):
        if S[j] == S[j+1]:
            return False
    return True

A while version of Fibonacci is:

def fibonacci():
    a = 0
    b = 1
    while True:
        # report value, a, during this pass
        yield a
        future = a + b
        a = b
        b = future

The recursion is defined as

$F_{0}=0$

$F_{1}=1$

$F_{n}=F_{n-2}+F_{n-1}$ for n>1.

A bad recursion version of Fibonacci is:

def bad-fibonacci(n):
    if n<=1:
        return n
    else:
        return bad_finonacci(n-2) + bad_fibonacci(n-1)

Let $c_{n}$ denote the number of calls performed in the execution of bad_fibonacci(n), then

The reason why it's so inefficient is because of the way the $n^{th}$ Fibonacci number, $F_{n}$, depends on the two previous values, $F_{n-2}$ and $F_{n-1}$. But after computing $F_{n-2}$, the call to compute $F_{n-1}$ requires its own recursive call to compute $F_{n-2}$, as it does not have knowledge of the value of $F_{n-2}$ that was computed at the earlier level of recursion. That is duplicative work. Worse yet, both of those calls will need to (re)compute the value of $F_{n-3}$, as will the computation of $F_{n-1}$.

A better version in Python is:

def good_fibonacci(n):
    if n <= 1:
        return (n, 0)
    else:
        (a, b) = good_fibonacci(n - 1)
        return (a + b, a)

It's good to visualize it in http://www.pythontutor.com/visualize.html#mode=edit